Scalable sparse matrix multiplication
 lost in translation
lost in translationWhen multiplying large matrices (mmul) the operation can turn out to be much more involved than initially intended. After some jokes about language translation I will show how to use Apache Spark to solve even very large matrix multiplicaiton problems using a framework for distributed computing.
lost in translation
When working most of the time in English (though me being a natively German speaking person) one sometimes forgets about the correct words in his or her mother tongue 😊.
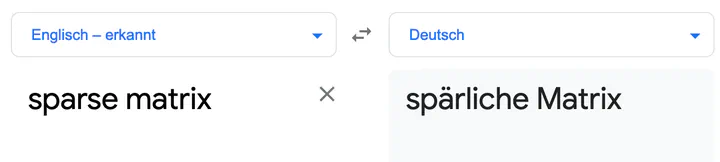
This happend to me for the word sparse matrix. With some colleagues at work (they had the same problem) we tried to translate the English term to German as poröse Matrix or schwamminge Matrix, both would mean in English porous or spongy matrix - none translation seemed correcct.
Even when using Google translate a translation which sounds wrong is given: spärlich. Google translate is converting sparse matrix to spärliche matrix (in German).
Interesting how this can be so complicated. Nonetheless, I will stick to the term sparse for the rest of the post.
When thinkig about this problem again I think that schwach/dünn besetzte Matrix might be a good translation, though it sounds pretty clumsy.
back to topic
When working on a project for my P.h.D. I wanted to perform an initially harmless looking matrix multiplication operation:
$ A * C * B$ where these matrices roughly have the shapes of:
- $A$ (223000, 250)
- $B$ (250, 223000)
- $C$ (250, 250)
and all were pretty sparse.
$A$ and $B$ are binary matrices. All elements are either 0 or 1. All three ($A,B,C$) are very sparse matrices, where a lot of values are missing.
In an initial draft I was following the basic sparse matrix dot product for scipy. Sadly, this failed as the matrix needed 3TB of RAM. And the computers accessible to me unfortunately do not have this amount of memory - so a solution was required.
After some tweaking of the data preprocessing code I could reduce the memory requirements to 330GB - but still, this was way too large compared with the currently accessible infrastructure.
Keep in mind you can rent some cloud computers with multiple TBs of main memory for a fairly cheap amount of $ per hour easily. However, given already access to a YARN cluster I was thinking about an even more scalable (distributed) solution. Maybe it is overkill - but computes nicely.
Step 1: first multiplication
The first part of the product: $A*C$ almost instantly computes using scipy or numpy. However, the second multiplication needs way too much memory for what my current infrastructure provides.
I have created a manual matrix multiplication using SQL in the distributed computing system Apache Spark.
Step 2: data preparation for spark
There are many sparse matrix formats with their specific advantages and disadvantages. A COO coordinate-based format however can be easily translated over into a database-like, sql-based scalable system like Apache Spark.
Therefore, I need to translate my matrices into such a format.
A data structure with columns like row, column, data is required.
When trying to translate the scipy sparse matrices I faced some struggles but figured out that the MXT format (apparently common in genomics) could nicely work.
My proposed solution for transforming the data is less than ideal (additional serializaiton), but works well enough to be quick to implement.
Given that the amount of data for the individual matrices is quite small it is not really problematic to perform this additional serialization (dear reader - if you know of a better solution please let me know).
To convert the matrices to the MXT format in parquet (a file format easily understandable Apache Spark) I use:
import numpy as np
import pandas as pd
from scipy.sparse import coo_matrix
a = np.eye(7)
a[2,5] = 66
a_coo = coo_matrix(a)
print(a_coo)
from scipy import io
io.mmwrite('sparse_thing', a_csr)
!cat sparse_thing.mtx
sparse_mtx_mm_df = pd.read_csv('sparse_thing.mtx', sep=' ', skiprows=3, header=None)
sparse_mtx_mm_df.columns = ['row', 'column', 'data_value']
sparse_mtx_mm_df['numpy_row'] = sparse_mtx_mm_df['row'] -1
sparse_mtx_mm_df['numpy_column'] = sparse_mtx_mm_df['row'] -1
sparse_mtx_mm_df
re_sparsed = coo_matrix((sparse_mtx_mm_df['data_value'].values, (sparse_mtx_mm_df.numpy_row.values, sparse_mtx_mm_df.numpy_column.values)))
print(a_coo)
print('****')
print(re_sparsed)
print(a)
re_sparsed.todense()
The so created (converted) sparse representation of the matrix in the form of a dense numpy_row,numpy_column,data_value pandas dataframe can be easily stored in a persistent storage volume of your choice such as S3 or i.e. HDFS as an parquet file:
pd_ra.to_parquet('hdfs://cluster/user/geoheil/mmul/A_mul_C.parquet', index=False, compression='gzip')
The second matrix is prepared in a similar way.
Step 3: distributed matrix multiplication
When performing a sparse matrix multiplication in SQL, I was inspired by 1. It turns out the mmul operation is quite simple in SQL - and just like scipy/numpy instant for small matrices.
SELECT a.row_num, b.col_num, SUM(a.value * b.value)
FROM a,
b
WHERE a.col_num = b.row_num
GROUP BY a.row_num, b.col_num;
However, due to the size of my matrices I need a more scalable solution. I decided to utilize Apache Spark (a framework for distributed computing) to improve the performance of the mmul operation. My approach was inspired by 2:
from pyspark.sql import SparkSession
# start spark
# this is a very naive basic default spark configuration
# you may need to (=must) fine tune it for your usecase
spark = SparkSession \
.builder \
.appName("Python Spark SQL basic example") \
.config("spark.some.config.option", "some-value") \
.getOrCreate()
# read both prepared (sparse, MXT formatted) parquet files from the persistent storage volume
A_mul_C = spark.read.parquet('mmul/A_mul_C.parquet')
B = spark.read.parquet('mmul/B.parquet')
However, the basic multiply function of 1 needs to be extended a bit (its inputs need to be optimized to be fast):
def multiply_matrices(A, B, enable_broadcast=False):
# BASED ON: https://github.com/Fokko/spark-matrix-multiplication/blob/master/multiply.py
# https://notes.mindprince.in/2013/06/07/sparse-matrix-multiplication-using-sql.html
A.registerTempTable("A")
if enable_broadcast:
# if matrix is small auto broadcast will do its job
B = broadcast(B)
B.registerTempTable("B")
return spark.sql("""
SELECT
A.numpy_row numpy_row,
B.numpy_column numpy_column,
SUM(A.data_value * B.data_value) data_value
FROM
A
JOIN B ON A.numpy_column = B.numpy_row
GROUP BY A.numpy_row, B.numpy_column
""")
mmul_result = multiply_matrices(A_mul_C.repartition(8000), B)
As spark is broadcasting small dataframes by default (I am using the lastest version 3.1.2 as per the writing of this post), the enable_broadcast is not mandatory - if your matrices are larger, a broadcast join is still recommended as the sparse matrices for sure are much much smaller than the computation you want to perform (= the computation and not the shuffle IO will take up the longest part of the computation).
Assuming broadcasting is enabled, the number of the input partitions will most likely be pretty small if not even 1 (yes a single one, as the initial sparse matrix file is so small).
Repartitioning the left side of the input is important ti increase the parallelism.
You must repartition the input - otherwise the matrix multiplication will not proceed as fast as possible - rather only minimal compute resources (most likely a single core) would be used.
However, when repartitioned to a suitable value spark will nicely perform the desired mmul computation.
For my particular usecase, roughly 224,000,000,000 rows of intermediate state needed to be calculated by spark. As I was using the broadcast join, however, only a minimal amount of shuffle IO was required for this gigantic sparse matrix multiplication.
Literature
My post here was inspired by: