Geospatial binning with hexagons on spark
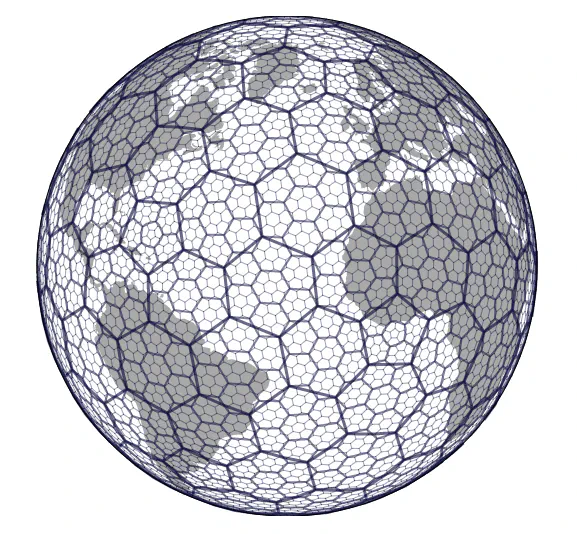 H3 enables users to partition the globe into hexagons for more accurate analysis.
H3 enables users to partition the globe into hexagons for more accurate analysis.Discrete global grid systems recently got quite some attention in the GIS community when Uber released H3 https://eng.uber.com/h3/.
It is a hexagonal spatial index. Neighbours can be accessed easily.
Several tasks are supported:
- spatial index
- spatial smoothing
- efficient spatial join
And a variety of libraries around the core c based code has been created. https://github.com/uber/h3-py-notebooks nicely demonstrates how spatial anomaly detection can be quickly built using the python API.
But wouldn’t it also be great to use this functionality in spark? They do provide a java library: https://github.com/uber/h3-java
Adding this to spark is straight forward. Using your build tool of choice first add a dependency to the jar.
// https://mvnrepository.com/artifact/com.uber/h3
compile group: 'com.uber', name: 'h3', version: '3.6.0'
or just start an interactive shell such as:
spark-shell --packages 'com.uber:h3:3.6.0'
and run:
import com.uber.h3core.H3Core
import org.apache.spark.sql.expressions.UserDefinedFunction
import org.apache.spark.sql.DataFrame
@transient lazy val h3 = new ThreadLocal[H3Core] {
override def initialValue() = H3Core.newInstance()
}
def convertToH3Address(xLong: Double, yLat: Double, precision: Int): String = {
h3.get.geoToH3Address(yLat, xLong, precision)
}
val geoToH3Address: UserDefinedFunction = udf(convertToH3Address _)
def createSpatialIndexAddress(result: String,
XLongColumn: String,
YLatColumn: String,
precision: Int)(df: DataFrame): DataFrame = {
df.withColumn(
result,
geoToH3Address(col(XLongColumn), col(YLatColumn), lit(precision)))
}
which can now be used as:
val df = Seq((1,2), (3,4)).toDF("x", "y")
df.transform(createSpatialIndexAddress("h3","x", "y", 7)).show(false)
+---+---+---------------+
|x |y |h3 |
+---+---+---------------+
|1 |2 |877545796ffffff|
|3 |4 |8775642cdffffff|
+---+---+---------------+
Other functions of the H3 library can be supported similarly. Using the hexagons greatly simplifies efficient spatial smoothing and aggregation (hexbinning).